Introduction

In the recent years, due to the democratization of the cloud technology, particularly scalable computing power and off-the-shelf machine learning services, the creation of supervised machine learning products can never be more straightforward. Roughly speaking, with the Auto ML services from major cloud providers, preparation of the labelled training data set is the only step needed.

However the supervised machine learning has one profound limitation when deployed into an interactive learning setting, for instance recommendation system. This limitation is attributed to the fact that the supervised model/agent/learner learns the latent pattern in the data using the labelled data and therefore lacks the ability to adopt with the external dynamical environment.

This limitation can be understood from the life cycle of model learning, as illustrated below:

The life cycle of model learning.
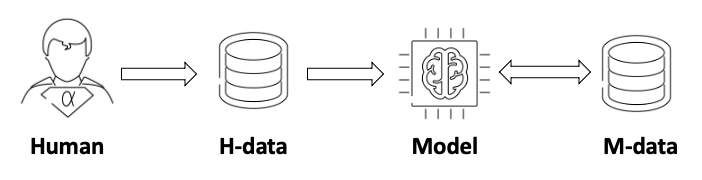
  • Step 1: Human generates the original data set: H-data
  • Step 2: The model is instructively trained based on the H-data
  • Step 3: The model generates data set M-data
  • Step 4: The model is iteratively and instructively trained with H-data or M-data

The above learning life cycle has a closed loop: data-model-deploy. In this process, the model will suffer in two scenarios:

  • If the human’s input is imperfect. For example, human’s decision is wrong.
  • If the environment the model is interacting with is non-stationary. For example, the person’s preference changes over time.

Reward is enough

The reward-is-enough hypothesis provides an elegant approach to solve the interactive machine learning problems and arguably the artificial general intelligence (AGI).

Reward-is-enough hypothesis: intelligence and its associated abilities, can be understood as subserving the maximization of reward. The agents that learn through trail and error experience to maximize reward could learn behaviors that exist most if not all of abilities in natural and artificial intelligence.

One realization of this reward-is-enough hypothesis is the reinforcement learning (RL) framework, which formalizes the goal-seeking problem as the maximization of rewards, as illustrated below.

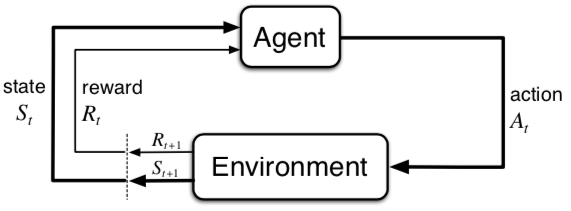
Reinforcement learning framework.

The agent sequentially takes an action against the environment and receives a new state of the environment and a new reward. The agent needs to make choices between exploitation and exploration when taking different actions. The goal of the agent is to achieve maximum rewards in a long run. More details about reinforcement learning.

The closed loop for reinforcement learning.

By adding the exploration logic, the agent will learn through trail and error experience without any prior-knowledge, which mitigates the imperfection of human knowledge as well as the non-stationary setting in certain real world environments.

Anatomy: from reinforcement learning to contextual bandit

The Markov decision process (MDP) is basically the mathematical realization of reinforcement learning. In the MDP, the numbers of Markov states in the real world setting are enormously huge. Therefore it typically requires enormous amount of training data. As a result, current full RL applications are limited within the simulation environment. For instance, video gaming where an emulator can be used to generate endless training data points.

To take advantage of both large amount of training data in the supervised machine learning and the nature of trail-and-error of RL, a few simplifications can be done to construct the so-called contextual bandit problem (CB):

  • Change the long-term rewards in RL to immediate rewards.

  • The state function of the environment is independent of the previous action token by the agent.

After the above simplifications, the RL diagram is broken down to the following one:

The contextual bandit problem.

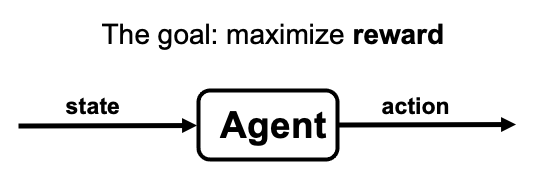
where a quad (state, reward, action_probability, action) can be passed through the agent to maximize the reward, namely cost-minimization.

Next the CB problem can be solved by doing following reductions:

  • Policy learning

  • Exploration algorithm

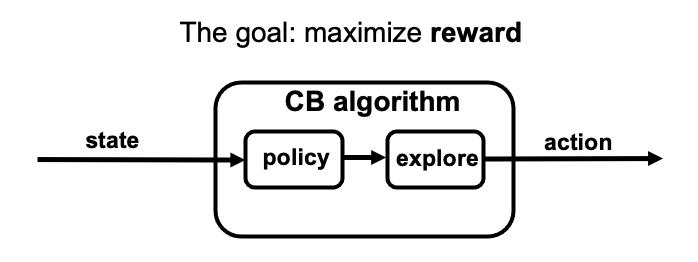
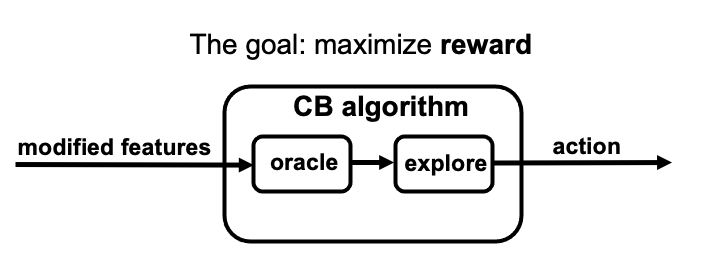
The reduction approach to solve the CB problem.

Finally optimization oracle, namely cost-sensitive classification oracle or regression oracle, can be invoked to learn the policy. Additionally, only the action token has been assigned with the cost. In order to fill in the costs of the never-token actions, different loss estimation methods can be applied to balance the input features, as shown later.

The optimization oracle and loss estimator.

Contextual bandit setup

The following description is adopted from A Contextual Bandit Bake-off

The stochastic (i.i.d.) contextual bandit learning problem can be described as follows. At each time step \(t\), the environment produces a pair \((x_t, \ell_t) \sim D\) independently from the past, where \(x_t \in \mathcal{X}\) is a context vector and \(\ell_t = (\ell_t(1), \ldots, \ell_t(K)) \in R^K\) is a loss vector, with \(K\) the number of possible actions, and the data distribution is denoted \(D\). After observing the context \(x_t\), the learner chooses an action \(a_t\), and only observes the loss \(\ell_t(a_t)\) corresponding to the chosen action. The goal of the learner is to trade-off exploration and exploitation in order to incur a small cumulative regret

\[R_T := \sum_{t=1}^T \ell_t(a_t) - \sum_{t=1}^T \ell_t(\pi^*(x_t))\]

with respect to the optimal policy \(\pi^* \in \arg\min_{\pi \in \Pi} E_{(x, \ell) \sim D}[\ell(\pi(x))]\), where \(\Pi\) denotes a (large, possibly infinite) set of policies \(\pi : \mathcal{X} \to \{1, \ldots, K\}\) which we would like to do well against.

Oracle

In the reduction approach, CB algorithms rely on optimization oracle:

  • cost-sensitive classification oracle (csc_oracle)
\[\arg\min_{\pi\in \Pi} \sum_{t=1}^T c_t(\pi(x_t))\]
  • regression oracle (reg_oracle)
\[\arg\min_{f\in \mathcal{F}} \sum_{t=1}^T \omega_t(f(x_t, a_t) - y_t)^2\]

In the offline-policy learning setting, full feed information is required to carry out the policy training. Below is three classic loss estimation methods:

  • Inverse Propensity Scoring (IPS) estimator \(\hat{\ell} _t(a) = \frac{\ell_t(a_t)}{p_t(a_t)} \mathbb{1}\{a = a_t\}\)

  • Doubly robust (DR) estimator \(\hat{\ell}_t(a) = \frac{\ell_t(a_t) - \hat{\ell}(x_t, a_t)}{p_t(a_t)} \mathbb{1}\{a = a_t\} + \hat{\ell}(x_t, a)\)

  • Importance-weighted regression (IWR) \(\hat \ell = \arg\min_{f \in \mathcal F} \sum_{t' \leq t} (f(x_{t'}, a_{t'}) \ell_{t'}(a_{t'}))^2\) considers the policy \(\hat{\pi}(x) = \arg\min_a \hat{f}(x, a)\)

In the online-policy learning setting, the oracles (csc_oracle and reg_oracle) can be optimized by incrementally updating a given policy or regression function after each new observation, using, for instance, an online gradient method. Additionally the loss estimation methods can be used to track the progressive validation loss in order to evaluate the model performance.

Exploration algorithm

Here some classic exploration algorithms (Details):

  • \(\epsilon\)-greedy

  • Greedy

  • Bagging

  • …

Contextual bandit in action: Vowpal Wabbit

Vowpal Wabbit (VW) provides a fast, flexible, online, and active learning solution that empowers you to solve complex interactive machine learning problems.

Reduction stack is the key: Vowpal Wabbit reductions Workflows

VW Reductions Workflows.

Here are three examples to understand the contextual bandit in Vowpal Wabbit:

Decision Service architecture

Putting a contextual bandits system into production environment requires a huge amount of engineering efforts, mainly because of the real-time nature of the system and careful-tweaking of the model. The white paper Multiworld Testing Decision Service provides a good starting point to implement and productionalize the contextual bandits system.

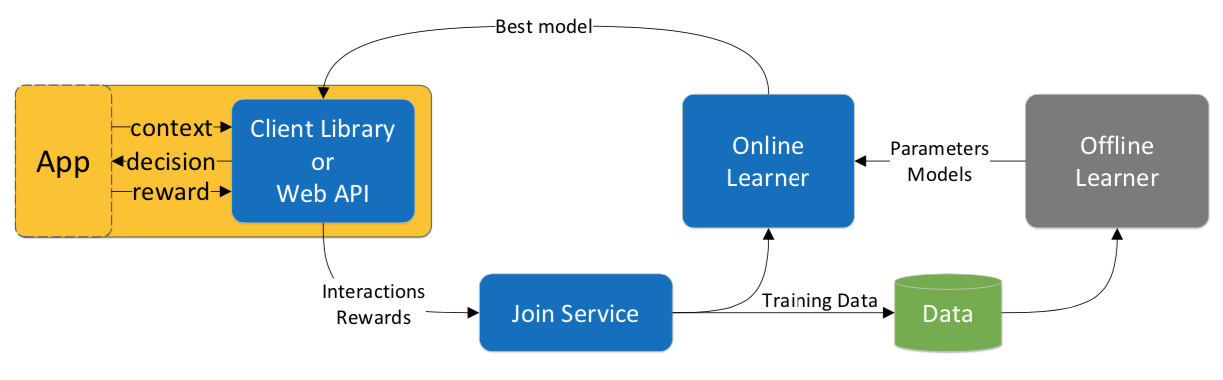
Decision Service architecture adapted from Multiworld Testing Decision Service.

Fortunately, Azure Personalizer provides an off-the-shelf contextual bandits service for content recommendation, which is basically the implementation of the white paper: Multiworld Testing Decision Service.

Summary

I discussed the limitation of instructive-based learning and one potential solution to overcome the interacting setting, namely contextual bandits. By leveraging both large amount of supervised learning data and exploration algorithms, the model/policy will be able to adopt to the dynamics of the real world.

Disclaimer: I never worked with a productionalized contextual bandits solution / VW. This blog is purely some notes from my learning.